今年寒假，学校安排我们读了一本书：《基本概念与运算法则》，这本书分为问题篇、话题篇、案例篇三大部。30个问题，引发对教学核心问题的思考；30个话题，拓展对教学核心问题的理解；20个案例，呈现对核心问题的教学设计。我重点结合教学谈谈对话题16数学证明的思维过程的理解和学习收获。

这个话题，重点讨论了数学命题是什么、数学证明是什么；数学命题是如何证明的、证明的依据是什么。

数学命题。在一般意义上，命题是一个能够进行肯定判断或者否定判断的语句，数学命题也是这样的一个语句。数学命题的核心，就是表示研究对象之间的关系。数学证明可直接判断或者数学推理。直接判断就是明确地对命题给出“肯定”或者“否定”的判断。推理是从一个命题判断到另一个命题判断的思维过程。

有关推理的分类与关系：

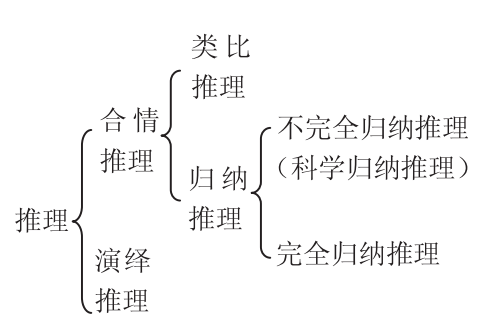
培养学生的数学推理能力是当今数学教育的一种核心价值取向， 2011 年数学课程标准特别指出：应将推理能力的发展贯穿于学生整个数学学习过程中。小学是推理教学的起步阶段，小学生的年龄特征与数学知识的特点，决定了小学数学中的推理及其教学具有阶段的特殊性。

（一）合情推理。

  “合情推理是从已有事实出发，凭借经验和直觉，通过归纳和类比等推断某些结果”。 联想、想象和迁移等心理活动与直觉思维常常与之相伴，其过程有时表现出思维方面的跳跃性和穿越感。 由于合情推理是从前提出发的“想当然”推断，其结论是或然的，不一定可靠（比如在认识长方形时，老师讲：长方形较长的边叫做长，那么较短的边……，学生常常 会抢先说：短）。尽管如此，但它对于数学学习依然十分重要，尤其是对于小学生。在小学数学推理中，合情推理所占的比重最大，它在探索思路，猜想、发现结论中经常使用，是小学生自主探索学习强有力的支持。合情推理可以分为类比推理和归纳推理。

例：关于“小数的认识”与“小数的意义”系列教学的推理片段 。

片段一（小数的初步认识）：

师：1/10 米可以写作 0.1 米。（前提）那么，2/10 米可以写作多少米呢？

生：2/10 米=0.2米，

师：5/10 米、9／10米呢？

生：5/10 米=0.5米、9／10米=0.9 米

师：你能自己举出类似的例子吗？（以上为类比推理）由此你能发现什么规律吗？ 谁来小结一下。

生：十分之几米都可以用小数表示；十分之几米等于零点几米。（结论）（以上为归纳推理）

（二）演绎推理。

   “演绎推理是从已有的事实（包括定义、公理、定理等）和确定的规则（包括运算的定义、法则、顺序等）出发，按照逻辑推理的法则证明和计算。”它以事实依据（包括已经证过的结论），经由合乎逻辑的推演和论证得出结论，前提与结论之间是必然的因果联系，因而用于对猜想的验证和结论的证明，如下面片段：

片段（小数的意义）：

师：十分之几米是零点几米，那么百分之几米呢？ 比如 29/100米、30/100 米和 5/100 米分别是多少米？

生：29／100 米=0.29 米……

师：对，我们已经知道一位小数表示十分之几，那么两位小数呢？

生：两位小数表示百分之几。

师：同意吗？ 对，这只是你们的推想，谁能举例证明呢？

生：比如以人民币为例，我们知道5分是0.05元（大前提），5／100 元是5分（小前提）所以 5／100 元=0.05元，也就是 5／100=0.05，这就证明了两位小数表示百分之几（结论）。

小学生处于由具体形象思维向抽象逻辑思维过渡阶段，并以具体形象思维为主。他们在思维方面的特征与数学知识抽象、概括，逻辑严密的特点，常常会导致认知过程中的冲突，这是困扰小学数学教学的普遍矛盾。因此我们可以容忍“不严格的清楚”、用推理替代“接受”。出 于建构新知需要的推理，在不违背结果的科性的前提下，当学生知识、经验、心智都不那么足够时，教师需要容忍他们在过程之中某个方面的些许“不严格的清楚”。演绎推理是这样，合情推理更应该是这样。因为在新知建构的起始阶段，有时“严格的不清楚不如“不严格的清楚”。数学中有许多的原理和定理，当原理和定理指导学生的行为，并使其按此办事时，原理和定理就成了规则。对于规则，老师们常常会采用“告诉”的方式教学，这样，学生的学习往往处于“接受”状态。其实，要改善学生的学习状态也不难，有时只要我们将规 则中最基本的一小部分知会于学生，然后就可以让他们通过推理，自己去知晓规则。

    数学的论证是有逻辑的，数学的体系是严谨的。